▼Coreform IGA Verification Manual
►3 Structural Modal Analysis
On this page:
3.1 Frequency Extraction
3.1.1 Frequency Extraction of Free Circular Plate
3.1.1.1 Objective
3.1.1.2 Geometry Description
3.1.1.3 External Interactions
3.1.1.4 Material Description
3.1.1.5 Method
3.1.1.6 Results
    contents  ← prev  up  next → 

3 Structural Modal Analysis

    3.1 Frequency Extraction

3.1 Frequency Extraction

    3.1.1 Frequency Extraction of Free Circular Plate

3.1.1 Frequency Extraction of Free Circular Plate

    3.1.1.1 Objective

    3.1.1.2 Geometry Description

    3.1.1.3 External Interactions

    3.1.1.4 Material Description

    3.1.1.5 Method

    3.1.1.6 Results

3.1.1.1 Objective

This verification problem shows that the Flex method is able to calculate several of the lowest fundamental frequencies of an unconstrained circular plate.

This problem is chosen as a verification problem because while exact solutions known they are quite challenging to derive and thus this problem represents, perhaps, the simplest structural modal problem for which known solutions exist yet it is still preferred, in practice, to produce a numerical approximation.

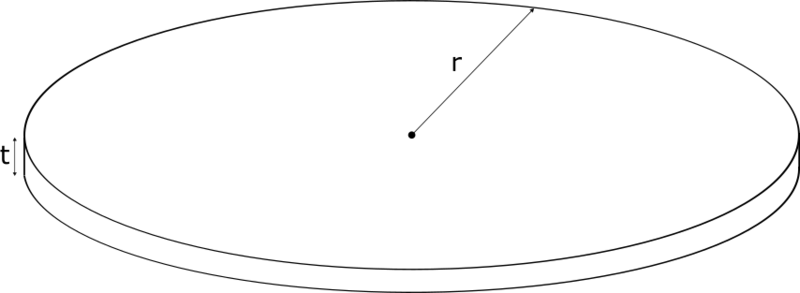
3.1.1.2 Geometry Description

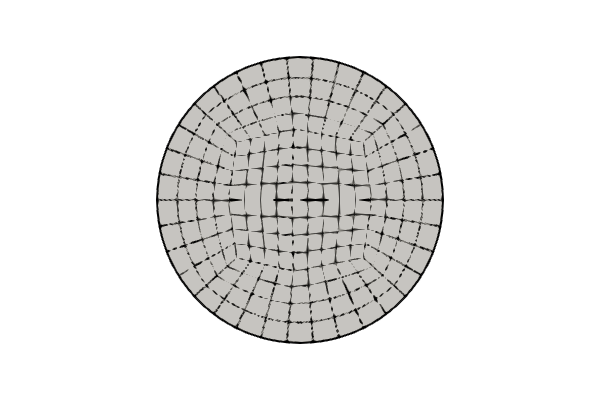
The geometry for this problem is a circular plate shown in figure 37. The parameters used to describe this geometry are provided in table 41.

Figure 37: Geometry of the circular plate.

Parameter

   

Value

t

   

0.01

r

   

1

Table 41: Non-dimensional values of geometric parameters.

3.1.1.3 External Interactions

There are no boundary conditions applied to the circular plate (i.e., “free vibration”).

3.1.1.4 Material Description

The non-dimensional material properties are given in table 42.

Dimension

   

Value

Young's Modulus

   

Poisson's Ratio

   

0.3

Density

   

1

Table 42: Non-dimensional material properties.

3.1.1.5 Method

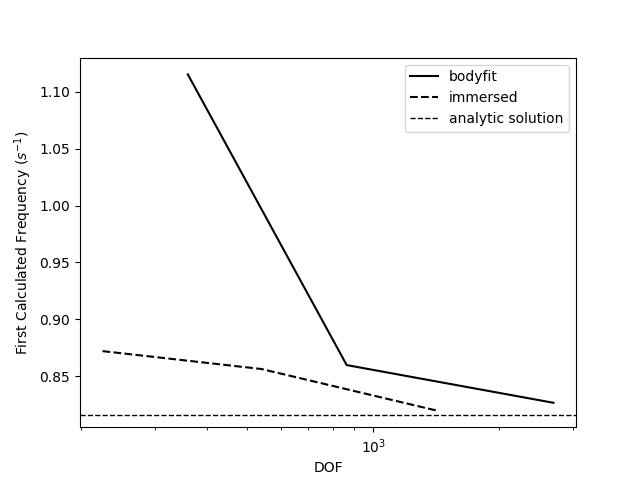
Results for this problem were computed using two approaches, each using Coreform IGA. One approach consisted of a traditional bodyfit-meshing approach while the other utilizes an immersed meshing approach. In addition, three levels of refinement were performed using each approach. These refinement levels are listed in table 43. A quadratic basis with maximal continuity was used in each case.

Refinement

   

Quadrature points

   

   

DOF

   

   

Immersed

   

Bodyfit

   

Immersed

   

Bodyfit

Coarse

   

243

   

324

   

225

   

360

Medium

   

864

   

1296

   

540

   

864

Fine

   

2943

   

5616

   

1413

   

2700

Table 43: Problem Size Comparison

The trimmed U-splines for each mesh are shown in figure 38.

Figure 38a: Immersed Affine (Coarse)

Figure 38b: Immersed Affine (Medium)

Figure 38c: Immersed Affine (Fine)

Figure 38d: BodyFit (Coarse)

Figure 38e: BodyFit (Medium)

Figure 38f: BodyFit (Fine)

Figure 38: Approach Comparison

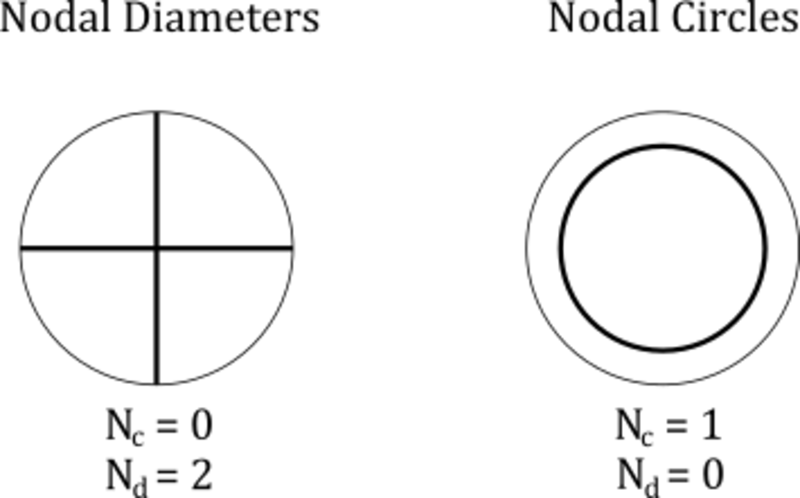
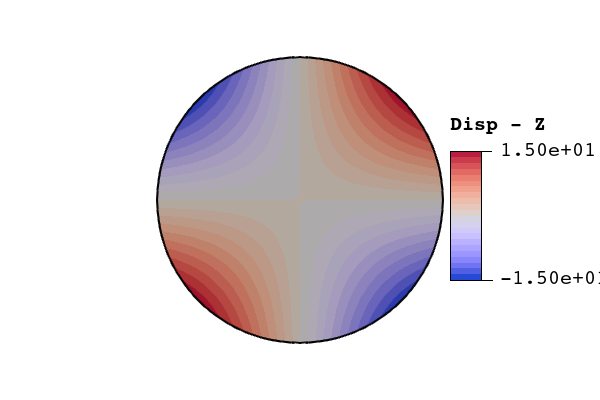
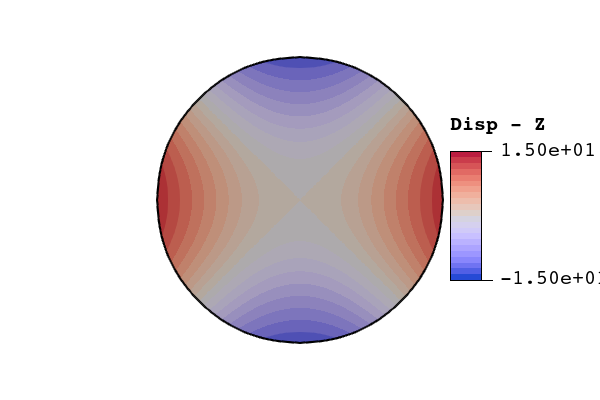
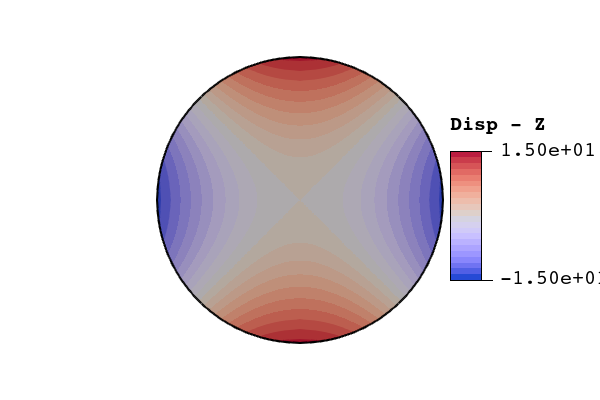
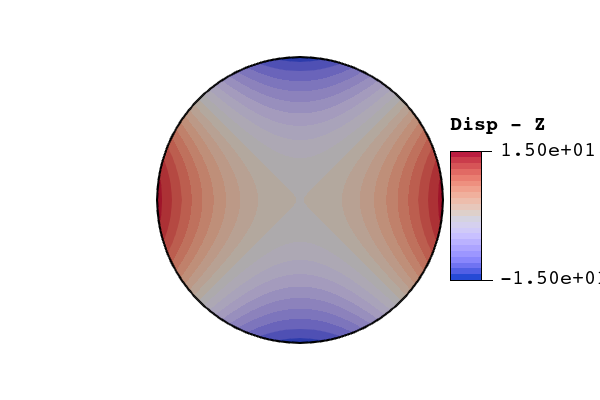
Results from both bodyfit and immersed meshes were compared against the analytic solution to the first fundamental frequency of a free vibrating circular plate. For a circular plate with radius , thickness , density , Young’s modulus , and Poisson’s ratio , the analytic solution for the natural frequencies in a vacuum are where is the non-dimensional frequency parameter and is the flexural rigidity. For a circular plate, the flexural rigidity is The non-dimensional frequency parameter is tabulated in the literature for values of and , where is the number of nodal circles and is the number of nodal diameters (see figure 39). A shortened list of calculated non-dimensional frequency parameters is shown in table 44.

Figure 39: Examples of nodal circles () and nodal circles (). The bolded lines represent the nodal lines of the associated eigenmode.

   

   

   

0

   

1

   

2

   

3.00052

0

   

2

   

5

   

6.20025

0

   

3

   

8

   

9.36751

0

   

4

   

11

   

12.5227

0

   

5

   

14

   

15.6727

   

   

   

1

   

1

   

3

   

4.52488

1

   

2

   

6

   

7.7338

1

   

3

   

9

   

10.9068

1

   

4

   

12

   

14.0667

1

   

5

   

15

   

17.2203

   

   

   

2

   

0

   

1

   

2.31481

2

   

1

   

4

   

5.93802

2

   

2

   

7

   

9.18511

2

   

3

   

10

   

12.3817

2

   

4

   

13

   

15.5575

2

   

5

   

16

   

18.722

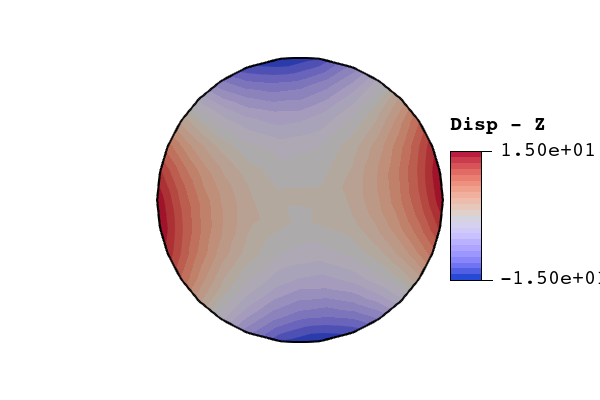
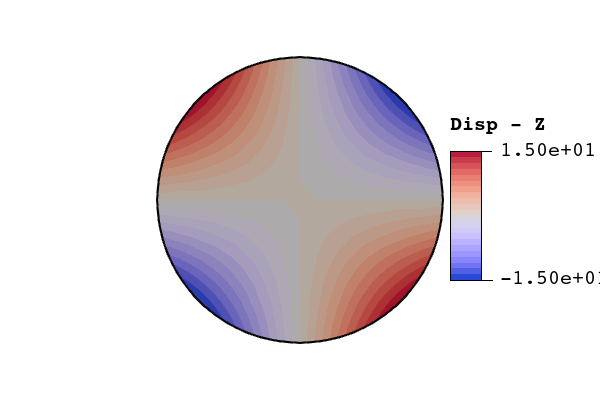
Table 44: Non-dimensional frequency parameters.

For the lowest fundamental frequency, , the non-dimensional frequency parameter is and its associated frequency is .

3.1.1.6 Results

Figure 40 shows the displacement patterns calculated for the first calculated frequency for both bodyfit and immersed approaches, for each level of mesh refinement. It is clear that for both bodyfit and immersed approaches, the and , which matches with the analytic lowest free vibration non-dimensional frequency parameter in table 44.

Figure 40a: Immersed Affine (Coarse)

Figure 40b: Immersed Affine (Medium)

Figure 40c: Immersed Affine (Fine)

Figure 40d: BodyFit (Coarse)

Figure 40e: BodyFit (Medium)

Figure 40f: BodyFit (Fine)

Figure 40: Approach Comparison

Figure 41 shows the mesh convergence of both bodyfit and immersed approaches.

Figure 41: Approach Comparison

Table 45 shows the calculated first frequency of the finest mesh for both approaches, as well as the relative error between each solution and the analytic solution.

Approach

   

Calculated Frequency ()

   

Relative Error (%)

Immersed

   

0.8200

   

0.47 %

Bodyfit

   

0.8266

   

1.29 %

Table 45: Relative error in fine mesh solutions for both approaches

Table 46 shows the solution characteristics of the finest mesh for both approaches.

Approach

   

Initialization Time (s)

   

Linear Equation Time (s)

   

Nonlinear Equation Time (s)

   

Solver Time (s)

immersed

   

1.19e-05

   

0.30

   

0.39

   

2.15

bodyfit

   

1.00e-05

   

0.30

   

0.95

   

1.98

Table 46: Solution characteristics for fine mesh solutions for both approaches

    contents  ← prev  up  next →